Square-1 / Cube 21

The Square-1, in the Czech Republic also known as the Cube 21, is a puzzle invented by Karel Hršel and Vojtěch Kopský around 1990. Number "21" refers to the century, meaning it is a cube for the 21^st century (freely translated). Especially in a solved state it may seem it is a variant of the Rubik's cube at first glance, but the opposite is true. In fact, it is a unique puzzle having exceptional features. That's why it is also recommended by Mensa Czech Republic as a puzzle developing spatial imagination, combinatorial skills and logical way of thinking.

On this page you will find:

Square-1 - notation
Square-1 - getting the puzzle into the shape of a cube
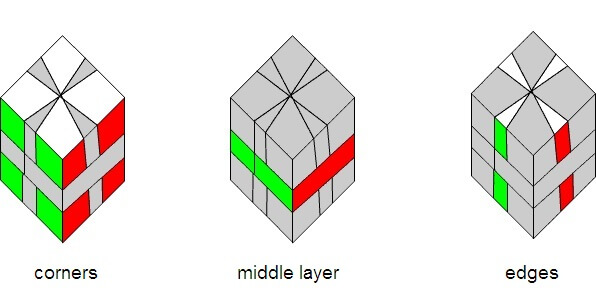
Square-1 - placing of corners into their layers
Square-1 - solving of corners
Square-1 - placing of edges into their layers
Square-1 - solving of edges
Square-1 - solving of parity problem and correction of the middle layer
world record videos

Square-1 - notation

Square-1 - getting the puzzle into the shape of a cube

In order to get the puzzle into the shape of a cube, proceed as follows: place two corners and all the edges into one layer, as shown after eighth move on video below. It is recommended to add the edges in successive steps. In other words, do not try to add them "all at once".

Tip: if you start by getting 6 corners into one layer, several different cases/configurations can occur in the second layer (actually the third layer since both the edges and corners can not be present in the second/middle layer) and only one of them is desirable (the same as shown on video below after a move no. 8). Hence it is better to start by adding all edges into one layer (in a manner so that we would reach the shape of the top layer after eighth move on video), because the other one will always be in a desired configuration by itself.

If you have the top and bottom layers in the shape of a square, and you only need to correct the middle layer, use one simple twist - see the following video.

Square-1 - placing of corners into their layers

Orient the corners, that is, separate them into their layers. All corners with a white sticker have been placed into one layer, while all corners with a yellow sticker have been placed into the second layer at the end of a video.

Square-1 - solving of corners

To permute (swap) two top right corners, use an algorithm which can be seen on video below. Those of you who know a T algorithm from the Rubik's cube blindfolded solving page will exult now because it is the same algorithm. Therefore, there is no need to learn it again. To permute bottom corners, simply turn the puzzle as a whole 180 degrees towards yourself (or the opposite direction) and after putting the corners into the right places (they must be at the top right positions) just apply the algorithm.

Let's have a closer look at one algorithm (see a video bellow). We see that it permutes two edges in the top layer and two edges in the bottom layer. This algorithm will be used in both phases regarding solving of edges.

Square-1 - placing of edges into their layers

The idea of this step is to properly set the edge from the bottom layer to the edge from the top layer, then execute the algorithm mentioned above and properly "split" both edges apart. In short, we will use conjugations.

In relation to the video: first two moves represent a "pairing-up of edges", third move is responsible for correct alignment of edges before executing an algorithm (to prevent permuting of the other edges than we want), then the algorithm mentioned above is being applied (moves 4 - 12), and finally the edges are being "separated" and put back into their appropriate layers. A swap of two edges in the bottom layer (see a video above) is the side effect of it. However, these edges are correctly placed (in relation to the layer to which they belong), hence they don't have a negative effect on the whole process.

Square-1 - solving of edges

By appropriate alignment of both top and bottom layer and after several executions (in this context, "several" can also mean one or zero - if you are lucky and all edges are already solved) of a 9-move algorithm mentioned above it is possible to solve all edges (except for one exception), thus possibly the whole puzzle. That exception is a parity problem, the word "possibly" in the previous sentence has been used because of a possibility to correct the middle layer.

Square-1 - solving of a parity problem and correction of the middle layer

Use two intuitive twists in order to correct the middle layer.

The last trouble you can encounter while solving the puzzle is called a parity problem. Let's take a closer look at it - parity problem refers to a state in which it is needed to permute (swap) only two edges on a Square-1 (more about a parity problem).

Perhaps the easiest (and most intuitive) case where this can be achieved is a shape in which 6 corners are in one layer, and all edges plus 2 corners are in the other layer - as being illustrated by moves 1 - 7 on video below. By eighth move a parity problem is being solved, since 1 6-cycle of corners is being applied. Moves no. 9 - 15 are inverse to the previous ones (their meaning is to get the puzzle into the shape of a cube) - so the conjugation principle is used. By moves 16 - 19 we solve again now scrambled layers. Afterwards we reach desired goal - after several executions of a 9-move algorithm mentioned above it is possible to get the puzzle into a state in which only two edges will be swapped.

World record videos

As a football has FIFA and athletics has IAAF, also the Square-1 has some sort of board that organizes the competitions worldwide. It is WCA - World Cube Association. Thus it can be officially competed in a solving of the Square-1. It is competed in two formats: single fastest solve of the puzzle and average solve. As an average, five consecutive times of one round are taken, the best and the worst time is not considered and from the remaining three times an arithmetic mean is calculated.

		event: Square-1 single solve
		name: Martin Vædele Egdal (Denmark)
		result: 4.59 s
		scramble: available upon request
		solution: available upon request
		puzzle brand: QiYi MoFangGe X-Man Design Volt M v2
		solving method: Vandenbergh
		personal opinion on used method: see below
		competition: Danish Championship 2020; 4-6. 9. 2020; Denmark

		event: Square-1 average solve
		name: David Epstein (Australia)
		result: 6.34 s
		scrambles: available upon request
		solutions: available upon request
		puzzle brand: QiYi MoFangGe X-Man Design Volt M v2
		solving method: Vandenbergh
		personal opinion on used method: see below
		competition: Solving in Sale; 10-11. 4. 2021; Australia

If you find a so-called speedcubing interesting, check out an article about where to buy a Square-1, what brand is the best and how to solve it faster.

Personal opinion on methods used in the world records

Square-1:

For the purpose of speedsolving I am aware of three Square-1 methods. First of them, which is the most commonly used method by far, is the Vandenbergh method. World records have been set almost always with it. Lars Vandenbergh was among the first ones who published the method on the internet.

But it's not the only one that has the potential to break the world record. I find the Baum as a competitive, however not very widespread method. The Screw method, which is an equivalent to the Roux method of a 3x3x3 cube, certainly deserves your attention as well.

The page was graphically improved by Jeremy Fleischman and Lucas Garron.