Three dimensions - too many or too little?

This article, along with the description of a parity problem, might seem quite weird to you. That's because I do mathematical stuff here without being a real mathematician. As a result, something which can look inconsistent and messy, or simply chaotic, is created. It is caused by two things.

First, I am not sure I fully understand given, a relatively complex, mathematical apparatus (i.e. I have no idea what I'm writing about). And second, it is closer to me to write in a pseudo-popular-educational style rather than in purely scientific form (so the difference between ambiguous meanings and unambiguous mathematical formulation is even deeper). Nevertheless, maybe you will find the following text and pictures as coming from a totally different world. Literally!

When 3 + 1 ≠ 4

Try to answer this question to yourself: "How many dimensional world do we live in?" Most of you probably answered by a number 3. Minority of you might choose number four, and only a small part of respondents gave another answer in my opinion.

Any point in our universe can be described by the x, y and z coordinates. Therefore, we are talking about 3D regarding the space, where D is a short for dimension. However, since one and the same point can be situated at various locations over the time, another dimension - time - is being introduced.

We can say that we live in a four-dimensional (i.e. 4D) world that consists of three spatial dimensions and one time dimension. Some physicists (many of them, needed to say) prefer to talk about (3+1)D rather than 4D. To be better oriented between (3+1)D and 4D, we won't further consider time parameter, only the spatial ones.

It turns out that some physical and mathematical models of certain events meet better a theoretical concept of more spatial dimensions than we are used to. Solutions to differential equations describing these events don't have to necessarily exist in 3D, but they may exist in 4D, 5D etc. Since there is nothing real that could be illustrated in 4D (and greater number of spatial dimensions) in our world, our brain has usually a problem to visualize and understand such concept correctly.

4D space can be explored from several points of view, and it is always advantageous to come from the analogies that we already know for 2D or 3D. Technically speaking, it is not possible to display a body with more than 2 dimensions on a screen from which you are reading this text (either a device screen or a list of paper in case you have printed the text). The reason is that both monitor screen and list of paper (not to mention human's retina) are also two-dimensional in ideal case (which is not met in reality; however, let's consider an ideal case in which it is met for the sake of simplicity). Our brain can handle a projection of a 3D body into 2D space, though - for example it is not a problem to perceive a Rubik's cube (on a paper or screen, i.e. in 2D space) or even play with it in the form of applet/simulator.

Surprising similarities

Let's ask another tricky question: "How to do an object in (n + 1)D out of its nD?". In other words, how to get something from 0D into 1D, from 1D into 2D, from 2D into 3D, from 3D into 4D etc.?

0D is a space in which there is no dimension. We can imagine it as an infinitesimal point. When you draw these two infinitesimal points, you can connect them through the dimension (first dimension is conventionally denoted as x). By that, 1D line is created.

When we draw one line above the other one appropriately, we can connect them through the second dimension (denoted as y). By that, 2D square is created. Let's continue in the same fashion: place first square behind the second one and connect them mutually through the third dimension (denoted as z). A cube is the result.

The same idea can be used, without any problem, even for the other dimensions. If we draw two mutually non-touching cubes, we can connect their corners by lines through the fourth dimension (denoted as w). By that, the 4D analogy of a cube, also known as the hypercube or tesseract, is created. It will be further familiarly designated as a 4D cube or simply NxNxNxN cube (in this case N = 1).

Conventionally it is given that x-axis goes from left to right, y-axis goes from bottom to top, z-axis goes from back to front and finally w-axis can be imagined as going from down from (sometimes the Greek term kata is used for that) to up toward (we can encounter the Greek term ana). All 4 axes are mutually perpendicular in a 4D space.

Fig. 1 - Tesseract construction

Properties of a 4D cube will be discussed later - they are not so obvious to see on Fig. 1. Now let's get back to notation for a moment. Measures of the first three dimensions are often appointed as length, height / depth and width - which applies to the cube, for instance. But how would you call a measure in case of 4^th dimension? In English, the word "trength" is used for that. Furthermore, in 2D we have a perimeter and area, in 3D we have a surface area and volume, but what do we have in 4D? In English, surface area maps to "surcell" (junction of the words surface and cell - see below) and volume maps to "bulk".

Last remark regarding notation: a 3D cube is composed of 6 sides (on Rubik's cube those are called faces), each of which has a square (i.e. 2D object) shape. A tesseract, on contrary, is composed of 8 sides (those are called cells in 4D) and each them has a cube (i.e. 3D object) shape.

Hypercube at close range

We have learned that the 4D analogy of a cube is composed of 8 cells. Each cell consists of a 3D cube with the same volume (similarly to each side on a 3D cube consists of a 2D square with the same area). It implies, among others, that all the lines on a tesseract are of the same length and in a mutual angle of 90° - which is impossible to express in 3D. That's why the "outer" cells on Fig. 2 (and next ones) are being distorted - deliberately compare it with the sides of a cube in 2D projection (and you should reach an analogy).

Fig. 2 - from left to right: 2D projection of 3D cube, 4D cube shown in 3D (in 2D projection)

The following Fig. 3 will say more than a thousand words, and it illustrates 4D (1x1x1x1) cubes (similarly to the right side of a Fig. 2).

Fig. 3 - 1x1x1x1 cubes

So why is Fig. 1 different from Fig. 3? It's due to the fact that Fig. 1 shows a tesseract being rotated in space. Statically it can be expressed via following chart (where the tesseract rotates around y and at the same time z axes).

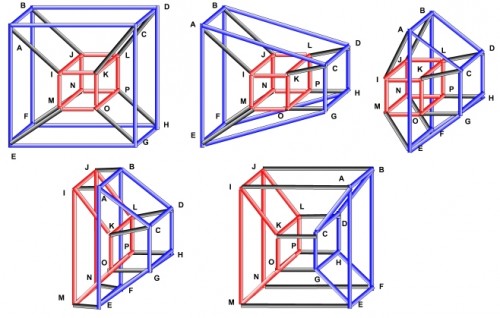
Fig. 4 - Static rotation of 4D cube

Previous figure can be dynamically (using animation) expressed via the left part of the next figure (the axes around which the body rotates remain the same, but a direction of rotation is reversed). The same, except for the x and at the same time z axes, can be seen on the right side.


Fig. 5 - Dynamic rotation of 4D cube

3D cubes can rotate around the x, y and z axes (see x move, y move and z move in a Rubik's cube notation). In case of rotation around the x axis, R and L rotate in place, while U, D, F and B faces rotate in a loop. Similarly, a 4D cube can rotate around the x and at the same time y axes, x and at the same time z axes, x and at the same time w axes, y and at the same time z axes, y and at the same time w axes, or z and at the same time w axes (then a pair of axes is called the plane). From a 3D point of view, (see Fig. 3, for example) the smallest cell will be denoted by a letter A and the biggest one by a letter K. The rest of the letters corresponds with a 3x3x3 cube notation. Then, in response to the video below, in case of rotation around the:

x and at the same time y axes the cells R, L, U and D rotate in place, while F, B, A and K cells rotate in a loop (see 0:00 - 0:30)
x and at the same time z axes the cells R, L, F and B rotate in place, while U, D, A and K cells rotate in a loop (see 0:30 - 1:00)
x and at the same time w axes the cells R, L, A and K rotate in place, while U, D, F and B cells rotate in a loop (see 1:00 - 1:30)
y and at the same time z axes the cells U, D, F and B rotate in place, while R, L, A and K cells rotate in a loop (see 1:30 - 2:00)
y and at the same time w axes the cells U, D, A a K rotate in place, while R, L, F and B cells rotate in a loop (see 2:00 - 2:30)
z and at the same time w axes the cells F, B, A a K rotate in place, while R, L, U and D cells rotate in a loop (see 2:30 - 3:00)

In other words: consider a common ant as a 2D creature (so the third dimension is neglected). If you place it on a cube, the ant can choose from 3 ways while going straight ahead and getting back to the starting position. These three mutually intertwined rings are denoted by the letters M, S and E on Rubik's cube. If we use letters as being abbreviations for particular faces, then we get R L F B, U D F B and R L U D. If you (as a 3D creature) will ever be placed on tesseract by a 4D alien, it might be useful to know that there are 6 mutually intertwined rings, each consisting of 4 cells - already mentioned F B A K, U D A K, U D F B, R L A K, R L F B, R L U D.

Don't let your own brain fool you, though - when a 4D cube is rotating, it may seem that the inner cell is smaller in terms of volume than the outer cell. As already stated, all of them are identical (when a 3D cube is rotating, the area of individual sides doesn't change either). Likewise, even when throwing a coin in the air, its volume is not changing, although the shape of a coin changes according to the scheme O→()→|→()→O from observer point of view. The same can be observed on the sides of a cube that rotates around one axis. Similarly, this is also the case for the cells on a hypercube. However, the inner cell is located at the position of the outer cell inside out during a rotation process.

What does it tell us? If we lived in a 4D world, from one perspective we would see the others as we are used to. But if the observed people turned, we would see their internal organs, while they would still be mutually touching each other. Perhaps doctors might be glad for such a view, but for the rest of the population it would probably look rather disgusting.

Personally, I find even more interesting an implication coming from Fig. 2. If we redraw it as seen on Fig. 6, we will find out that our brain is trying to fool us again!

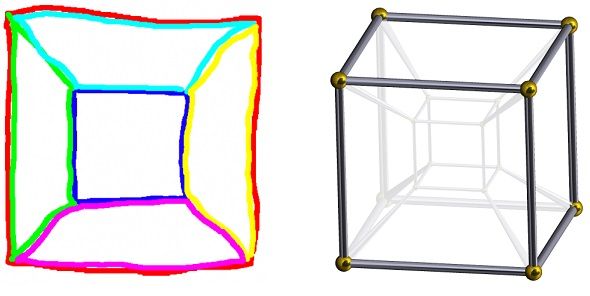
Fig. 6 - Projection of 3D and 4D cubes (into 2D)

On the left we see a 3D cube being projected into 2D. Individual sides (which are transparent in this case) are distinguished by color. The figure can be perceived as follows: the red side is closest to the eye of an observer, while the dark blue side is the farthest one. On the right we see a 4D cube illustrated in 3D (and projected into 2D). The closest cell toward the observer is denoted, remaining 7 cells are color-faded (i.e. they are shown in gray).

On the left cube, there are 5 sides behind the red color, so these sides will be drawn inside the red square. They are at the back in 3D space, therefore they are inside in a 2D projection. For a tesseract on the right, there are 7 color-faded cells behind the outer cell, therefore these cells are drawn inside (similarly to a cube on the left). Analogically, these 7 cells are at the back (but this time in fourth dimension) and that is the reason why they are entirely inside in a 3D representation. Although our brain tries to tell us that 7 cells are inside, in reality (i.e. in 4D) they are outside!

Another way how we can imagine a cube and the analogy of a 4D cube is to use a net. Well-known form of a hopscotch and the relations between the sides of a cube in 2D are shown on the left side of a Fig. 7. In the center part, there are shown the relations between the cells in 3D in case of a tesseract. Colored lines indicate touching parts of stated objects in both cases. Rightmost diagram can be, as a matter of interest, compared with a Fig. 1.

Fig. 7 - Nets of 3D and 4D cube

You may wonder: "OK, as long as it is possible to unfold a 3D cube into 2D net, maybe it would be possible to unfold the cells in 3D into 2D net as well". And you're right, it can be really done. What seems to be intuitive execution of this task is illustrated on the left side of the next figure.

Fig. 8 - Incorrect and correct interpretation of 2D net of 4D cube

Unfortunately, it's not a correct representation of tesseract's 2D net because it is composed of only 24 squares. You may notice that two sides of a 3D cubes in the centre part of a Fig. 7 are always shared by two cells, so from 6·8 = 48 squares will become (6·8)/2 = 24 squares - see the right part of a Fig. 8.

Before we go further, perhaps you will agree with the following statement: when you think you understood a 4D space, you realize that it is still a little bit more complex than you thought till now. It is tempting to paraphrase Socrates here with his "I know that I know nothing". Personally, it seems to me that the more I know about a 4D space, the more I actually don't know about it.

4D Rubik's cube

Until now, only the 4D analogy of a cube has been mentioned. However, a 3x3x3x3 Rubik's cube is more interesting in terms of combinatorial puzzles. Classical 3x3x3 Rubik's cube in a solved state can be seen on the left side of a Fig. 9. On the right, there is a 4D Rubik's cube, also in a solved state.

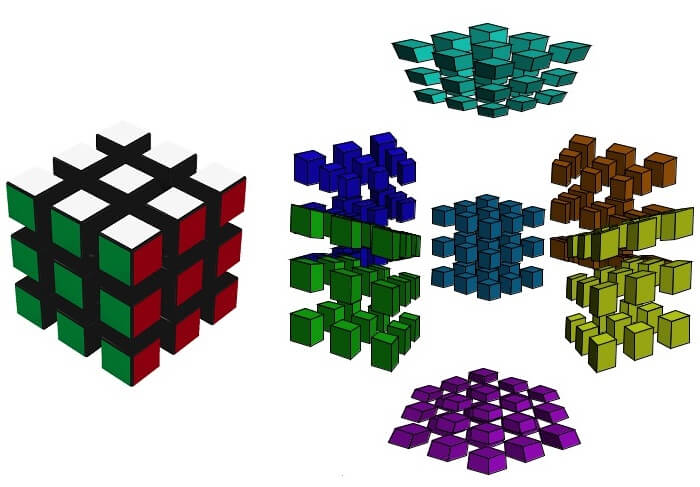
Fig. 9 - Solved 3x3x3 and 3x3x3x3 Rubik's cubes

You may be wondering: "where the hell is eighth cell on a 4D cube"? The answer is (il)logical, as it is common for four dimensions: it is connected with all six surrounding cells (except for the water-colored one located in the middle), but on the opposite sides than in case of a water-colored cell - it is simultaneously on the left and on the right, at the front and at the back, at the top and at the bottom. Since it is difficult to illustrate this concept in 3D in a given view (plus it would be extremely confusing for our brain in a selected projection - see Fig. 20 below), eighth 3x3x3 cell is simply invisible. However, a video below Fig. 5 implies that it can get to the current position of a water-colored cell by appropriate double rotation of the puzzle as a whole, or it can get to the position of any other cell by appropriate single puzzle rotation.

You can notice that each cell has one color (similarly to solved state of a 3x3x3 Rubik's cube, where each face is one-colored as well). While one face of a 3x3x3 cube consists of nine (3·3) 2D stickers, one cell of a 3x3x3x3 consists of 27 (3·3·3) 3D stickers. Generally, there are (D-1)-dimensional stickers on the "faces" of a D-dimensional cube.

Recall that a 3x3x3 cube is composed of:

6 one-colored centers
12 two-colored edges
8 three-colored corners

A 3x3x3x3 4D cube is composed of the following pieces:

8 one-colored centers
24 two-colored hyper-centers
32 three-colored hyper-edges
16 four-colored hyper-corners

Fig. 10 - Left: highlighted center piece; Right: highlighted hyper-center piece

In both cases (3x3x3 as well as 3x3x3x3) the pieces denoted as "centers" are fixed relative to each other. Therefore, they determine the color of a face (cell, if you will).

Fig. 11 - Left: highlighted hyper-edge piece; Right - highlighted hyper-corner piece

Why just the numbers 8, 24, 32 and 16 in terms of a number of pieces? Well, because they came out when substituting into general formula :-). But first a bit of theory: generally speaking, D-dimensional Rubik's cube in the form of 3^D has D+1 piece types containing 0, 1, 2 ... D different colored stickers. There is 1 piece having 0 stickers in case of a 3x3x3 (on a real cube it is the center-axial cross), 6 pieces having 1 sticker, 12 pieces having 2 stickers and finally 8 pieces having 3 stickers. Promised formula for a number of piece types in dependence on a number of different colored stickers for a Rubik's cube in the form of 3^D is:

where N represents the number of stickers on a given piece type, D denotes the number of puzzle dimensions and exclamation mark is a factorial. Out of interest, there is also included an overview table for D and N values in a range of 0 through 10.

To generalize the formula written above, we can use a formula for a number of piece types in dependence on a number of separating cuts in one direction per face + 1 (i.e. 3 separating cuts in one direction + 1 = 4 for a 4x4x4 Rubik's cube, 4 separating cuts in one direction + 1 = 5 for a 5x5x5 Rubik's cube, etc.) for a Rubik's cube in the form of A^D (where A represents the number of separating cuts in one direction per face + 1). Then we can write:

Rubik's cube 3x3, 3x3x3, 3x3x3x3 and 3x3x3x3x3

Fig. 12 - Rubik's cubes 3x3, 3x3x3, 3x3x3x3 and 3x3x3x3x3

It can be numerically proved that a 3x3x3x3 Rubik's cube can have nearly 1.8·10¹²⁰ distinct states / configurations / combinations (compared to "only" 4.3·10¹⁹ in case of a 3x3x3 cube). For a 4x4x4x4 tesseract, there are already more than 1.3·10³³⁴ distinct configurations (in comparison with "only" 7.4·10⁴⁵ in case of a 4x4x4 cube). A 5x5x5x5 cube can be in one out of more than 8.2·10⁷⁰⁰ distinct states (compared to 2.8·10⁷⁴ in case of a 5x5x5 cube). The number 8.2·10⁷⁰⁰ is unimaginable (certainly we don't come across with such big numbers every day), but it is still nothing in comparison with the number of combinations for a 150x150x150 Rubik's cube. On contrary, a 2D 3x3 Rubik's cube shown above has only 4 possible orientations and can not be even scrambled.

I believe that solving of a 3x3x3x3 is, on principle, the same as for a 3x3x3 cube (at least in terms of commutators and conjugations) - it is indicated by a fact that some experts can even solve 4D puzzles while being blindfolded (in such case a puzzle simulator will change all stickers to gray after the first move is made). Nevertheless, since there are also other piece types in 4D analogy (with the "hyper" prefix), interesting situations can occur while solving. One of them is illustrated on a figure below. It deals with a wrong orientation (4D rotation, if you will) of just one hyper-corner, which was created by a combination of two 3D rotations. The first one has been performed around the dark-blue "axis" (i.e. x axis) and the second one has been done around the water-colored "axis" (i.e. y axis), resulting in a swap of green and dark-blue stickers as well as light-blue and water-colored stickers.

On the other hand, we know all of it from a 3x3x3 cube. Only 2D rotations around the 3D axes are available on it. If, for instance, we want to orient / rotate UFR corner, we can execute an F move, followed by an R move. Considering just corners, these two 2D rotations result in a 3D rotation of a corner at the UFR position. The only difference between 3x3x3 and 3x3x3x3 is that for the latter, only 3D rotations around the 4D axes are available. The idea, however, remains the same - execution of two 3D moves that form a 4D orientation / rotation of a hyper-corner.

Fig. 13 - Solved puzzle except for 1 hyper-corner

More monstrous monstrosities

If you find solving of the 4D analogy of a 3x3x3 Rubik's cube beneath your dignity, you can add another dimension (via technique which can be seen on Fig. 1 - by combining two tesseracts) to create the 5D analogy of a 3x3x3 Rubik's cube, which will have a total of 810 stickers. We can continue in this trend no problem, thus we can make a 6D or 7D Rubik's cube (whose constructions, as well as relations among individual pieces, I can't personally imagine yet).

Supposedly, a 3x3x3x3x3x3x3 Rubik's cube in a solved state is illustrated on Fig. 14. Well, at least 7 out of its 14 faces (where as one face a 3x3x3x3x3x3 Rubik's cube is meant).

Fig. 14 - Solved 7D 3x3x3 Rubik's cube

From its solved boring state we can scramble it. Then we would see something like what is shown on Fig. 15.

Fig. 15 - Scrambled 7D 3x3x3 Rubik's cube

If you think that finding of a piece to be solved is almost a superhuman task in this tangle of colors, I have no choice but to agree with you. What's more, one thing is finding that piece and another thing is to really solve it. Only a handful of people on Earth did it for all 2 172 moving pieces that occur on the puzzle, which means they correctly placed and oriented all 10 206 visible stickers (both mentioned values can be found in a table above).

7D analogy of a 3x3x3 Rubik's cube has more than 3.3·10⁸⁹³⁵ distinct states, and of course, this toy is solved in only one of them.

7D analogy of a 5x5x5 Rubik's cube also belongs to super-duper gizmos for sure. It contains 78 110 moving pieces and 218 750 visible stickers. The number of combinations for this pet has almost 227 000 digits (roughly). A 3x3x3 Rubik's cube with its 20 digits seems more than ridiculous here.

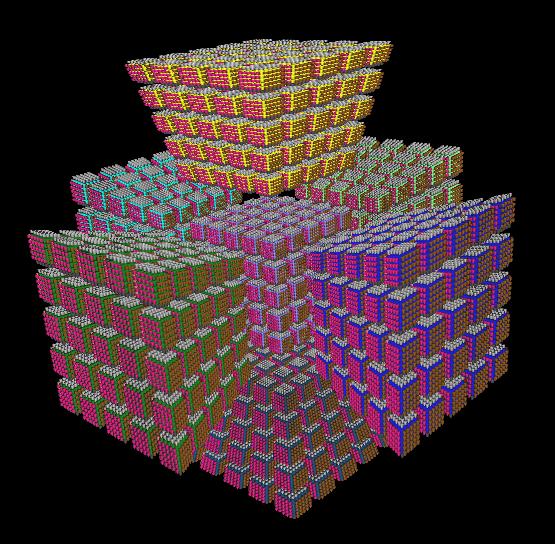
Fig. 16 - Solved 7D 5x5x5 Rubik's cube

Allow me to make one final point to conclude. We have already seen the 4D analogy of a Rubik's cube. How about showing also a 4D analogy of the Megaminx? It consists of 120 cells and each of them has a shape of a Megaminx (i.e. dodecahedron). We will find 2 641 pieces, 7 560 stickers and 2.3·10⁸¹²⁶ distinct configurations on it. How big is this number? First of all, big enough. Second of all, try to imagine that every particle in the universe is a tiny universe with the same number of particles as in our universe. That's much more particles, right? Now, imagine that all the particles in all the universes are just another universe for the same number of particles as in our universe. That makes a really big number of all those particles, doesn't it? Now just repeat the whole process more than 100x and you will get close to the number of combinations that can occur on the 4D analogy of a Megaminx.

Fig. 17 - Solved 4D analogy of Megaminx

You can see scrambled puzzle below. For the sake of better clarity, some parts of it were cut away.

Fig. 18 - Scrambled 4D analogy of Megaminx

Room for brain-teasing

Simple thought was an impulse for writing up this entire article. It occurred to me that if I make one face of a Rubik's cube partially transparent, I will be able, at a certain puzzle rotation, to see all 6 faces which appear on a cube in just one look. At that time, I was looking at the 4D analogy of a cube simulator, and so it was only a small step to take for getting an idea of how to see the whole 3x3x3x3 hypercube also in just one look, without a need to rotate the puzzle through 4^th dimension.

Over the time, it turned out to be not so easy task. Therefore, I decided it would be easier to see a 3x3x3x3 to be rotated around its axes at first, similarly to the case of a 1x1x1x1, as it can be seen on Fig. 5. Although I don't see any reason why such concept should be impossible to be drawn / animated, I am not able to make it happen. Thus the second thought (i.e. a 3x3x3x3 rotation around two of its axes) is still waiting for a confirmation (or refutation, if you will).

Let's get back to initial thought - how to see the whole 4D puzzle without a need to rotate it in the fourth dimension. E.g. Fig. 19, where there is the 4D analogy of a 2x2x2 Rubik's cube, may serve for this purpose. Assuming that (w, x, y, z) are coordinate axes, the red cell (see a left part of a figure) has (1, 0, 0, 0) coordinates, while the olive cell (see a right part of a figure) has (-1, 0, 0, 0) coordinates.

Fig. 19 - 2x2x2x2 Rubik's cube

These two views allow to see all 8 cells, and their mutual relations are also clear. But I originally wanted just one look. In accordance with the first paragraph under a Fig. 9, we can draw eighth cell on a tesseract as follows:

Fig. 20 - Transparent cell on a 3x3x3x3 Rubik's cube

As already mentioned, our brain is not predetermined to easily recognize the relations of the cells in a tesseract in a case where one cell will be partially transparent. That's why I wasn't satisfied with this view either. Then my friend Brandon showed me another projection screen in which one can see all 8 cells, while none of them is transparent.

Fig. 21 - All cells of 3x3x3x3 Rubik's cube in one view

Even though I know what I see, I admit frankly that I am not able to interpret it. Like everything which was said until now would suddenly become false. 4D rotation, which simply can not be understood by our (at least my) brain, is to blame for that. I wish "classical shape" could be preserved for this view, unlike this pyramid-like monster... If nothing else, it can be nicely seen that no cell lies inside another cell (in contrast to e.g. Fig. 20).

I find most illustrative to display all 8 cells in one view by means of a net being composed of a 3D 3x3x3 cubes.

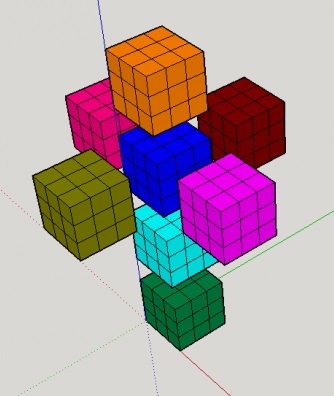
Fig. 22 - 8 cells in the form of 3D net

As the biggest advantage of this projection I find a possibility to rotate the puzzle in a 3D space - which is an activity that can be perceived by our brain without any problems. Moreover, all cells are always visible in just one look. By that the goal, which I originally wanted to achieve, is achieved.

Since 9 (3·3) pieces are moving when a move (U, for example) is executed on a 3x3x3 Rubik's cube, one move on a 4D Rubik's cube results in a movement of 27 (3·3·3) pieces. These are, in response to Fig. 22, shown on Fig. 24 (4D analogous move to a U move known from a 3D cube has been made there). If you do a face turn on a 3x3x3 Rubik's cube, some of the colored stickers, which are adjacent to a given face, will also move - as it can be seen from Fig. 23, where the green face is closest to us when looking from above, and a U' move has been executed.

Fig. 23 - Net of 3x3x3 Rubik's cube after 1 turn

If you do a cell turn on a 3x3x3x3 cube, some of the colored stickers, which are adjacent to a given cell, will also move. Recall that center piece remains in its place while doing a turn - it applies to both puzzles.

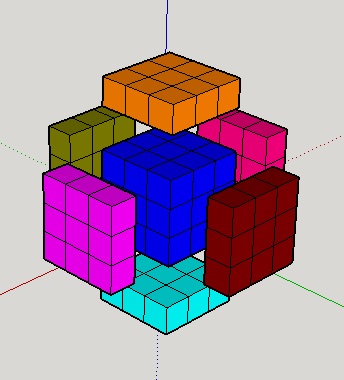
Fig. 24 - 27 moving pieces in 1 turn on 3x3x3x3 cube

My own idea (I'm not sure if it is even feasible) is to introduce a view in which there are only 7 out of 8 cells visible, and eighth one is displayed without a need to make a puzzle rotation in the fourth dimension. Since it's not a problem to draw 7 cells into a projection, it remains to answer the question how to implement eighth cell into this concept. We can put multiple colors on one sticker in case of a 3x3x3 Rubik's cube. If we do so, the Supercube will be made.

Fig. 25 - 3x3x3 Supercube

Ask me how would look a 3x3x3x3 in the form of a Supercube - I don't know. However, in a solved state, with regard to Fig. 22, the green cell wouldn't have to be drawn at all (see e.g. third picture from left on Fig. 12 - the green cell is hidden / invisible anyway). Nevertheless, it would be needed to put this green color on some other puzzle pieces (except for those with blue stickers). In addition, the moves would then look quite messy - after each of them, the colors being on individual pieces would be changed. In other words, one and the same piece would contain certain colors after a turn no. 1, but after a turn no. 2 (view angle at the puzzle would remain unchanged) the colors on it would be different. It is kind of similar to NxNxNxN (where N > 1) rotating tesseract - although I don't see a reason why it shouldn't work in theory, I can not imagine it factually.

When two dimensions are too many

Last chapter will proof that 3D objects can be unusually expressed in 2D. Fig. 23 showed widely used 2D net of a 3x3x3 Rubik's cube. Have you ever thought that it can be also expressed in a way as presented on the left side of a Fig. 26 (there is a sphere puzzle shape instead of a cubical one)? On the right there is a hint how such representation actually originated.

Fig. 26 - Unconventional representation of 3x3x3 Rubik's cube

We can draw the Megaminx or 5x5x5 Rubik's cube in the same manner.

unconventional net of a 5x5x5 Rubik's cube and Megaminx

Fig. 27 - Nets for Megaminx and 5x5x5 Rubik's cube

The figure below shows a net of the Petaminx, which is a four-layered Megaminx. It is followed by illustrative video, which is used to get a general idea of what pieces are being moved when making a turn.

Fig. 28 - Unusual net of Petaminx

Not so long ago I made a remark in front of my friend Tom (who has otherwise nothing in common with combinatorial puzzles) that I am trying to understand a 4D cube. His reaction blew my mind completely. He replied something in a way that he succeeded to draw a 16D cube on a paper.

I was thinking "right, if only you were telling the truth...". Next day he showed me a sketch he was drawing in one hand, while he was replying to some e-mail simultaneously, using the other hand. That's why his inartistic doodle is perfectly justifiable.

Fig. 29 - Cube in 3D and 2D

Above we see something which is intended to be a cube. Four corners are denoted by dots, other four corners are not denoted since there was no time to do so :-). Below, there are all 8 dots representing all 8 corners. They are connected by edges (above in the shape of a line, below in the shape of a half-circle). We can notice each corner is connected with three others and that's the reason why three half-circles come always from one dot. That's all. Simple and elegant.

By drawing of two such dots and half-circles mixture and by creating of other half-circles which connect appropriate (hyper) corners through another dimension, a 4D cube will be constructed. Although Tom's interpretation is much more difficult to imagine (similarly to Fig. 1) - for example just because the half-circles are not proportional in size, or due to the fact that all corners lie on a single line - I must admit he was probably right. By this way it is indeed possible to construct a cube of many dimensions. He said he ended up with 16D because then there was no room on a paper yet (he said he used A3 format).

There are many 3x3x3 Rubik's cube simulators. For some of them, we can see all its 54 stickers in one look - e.g. Fig. 30 on the left. In contrast, there are also more "realistic" simulators which don't allow us to see all puzzle pieces in one look - e.g. Fig. 30 on the right.

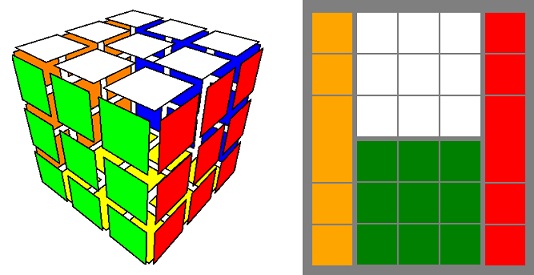
Fig. 30 - Two different Rubik's cube simulators

On the right side of a Fig. 30, the front face is green and the top face is white. Orange and red stickers are also in there, while 2 big blocks represent two colors of corner stickers. As a result, we can observe 5 edges, 2 centers and 2 corners (as well as some parts of 2 other edges and 4 other corners) in one look.

Although neither case can be fully identified with a view known from reality, the fastest people can solve both projections in a few seconds. It, by the way, also applies to the real puzzle.

The page was graphically improved by (links valid as of March 9, 2015):

Fig. 1 - https://en.wikipedia.org/wiki/Hypercube
Fig. 2, 3 (right) - http://cr4.globalspec.com/blogentry/23006/Rubik-s-Hypercube-Newsletter-Challenge-August-2013
Fig. 3 (left) - http://www.shapeways.com/product/Z2JLWWP3X/hypercube-a
Fig. 4 - http://www.kastellorizo.org/puzzles/4Ds
Fig. 5 left - https://cs.wikipedia.org/wiki/%C4%8Ctvrt%C3%BD_rozm%C4%9Br
Fig. 5 right - http://www.mathematik.com/4DCube/4DCubePovray.html
Fig. 6, 8 (left), 13, 19, 20, 21, 22 - http://twistypuzzles.com/~sandy/forum/viewtopic.php?f=8&t=27375
Fig. 7 (left and in the centre) - http://forums.xkcd.com/viewtopic.php?t=21376
Fig. 7 (right) - https://en.wikipedia.org/wiki/Four-dimensional_space
Fig. 8 (right) - http://www.magic-squares.net/c-t-htm/t_unfolded.htm
Fig. 9 (left) - https://www.randelshofer.ch/cubetwister
Fig. 9 (right), 10, 11 - http://superliminal.com/cube/cube.htm
Fig. 12 - http://www.gravitation3d.com/magiccube5d/anatomy.html
Fig. 14, 15, 16 - http://astr73.narod.ru/MC7D/MC7D.html
Fig. 17, 18 - http://www.gravitation3d.com/magic120cell/index.html
Fig. 24 - private correspondence with user rayray_2561 at http://www.twistypuzzles.com/forum
Fig. 25 - https://sites.google.com/site/twistykon/home/new-in-2011
Fig. 26, 27, 28 - http://www.gravitation3d.com/magictile
Fig. 29 - friend Tom
Fig. 30 (left) - https://www.ocf.berkeley.edu/~jfly/projects/qqTimer/qqTimer.htm
Fig. 30 (right) - http://mzrg.com/js/qcube-v2.html