Kontakt

Tři rozměry - hodně nebo málo?

Tento článek, společně s popisem problému parity, na vás možná zapůsobí přinejmenším dost divně. To proto, že zde fušuju do řemesla matematikům, aniž bych byl jedním z nich. Ve výsledku tak vzniká cosi, co se může zdát nekonzistentní a neuspořádané, zkrátka chaotické. Příčinou jsou dvě věci.

Jednak si nejsem jist, že danému, poměrně složitému, matematickému aparátu zcela rozumím (tzn. vůbec nevím, která bije) a za druhé je mi bližší psát v pseudo-populárně-naučném stylu raději než ve formě ryze vědecké (čímž se rozdíl mezi dvojsmyslnými kontexty a jednoznačným matematickým formulováním nadále prohlubuje). I přesto možná shledáte další řádky a obrázky jako pocházející z úplně jiného světa. A to doslova!

Když 3 + 1 ≠ 4

Zkuste si v duchu odpovědět na následující otázku: "V kolika rozměrném světě žijeme?" Většina z vás asi odpověděla číslovkou 3. Menšina mohla zvolit čtyřku a jinak dle mého názoru odpověděla jen nepatrná část respondentů.

Jakýkoliv bod v našem vesmíru může být popsán souřadnicemi x, y a z. Proto v souvislosti s prostorem mluvíme o 3D, kde D znamená dimenze (česky rozměr). Protože se ale jeden a ten samý bod může v čase nacházet na různých místech, zavádí se další dimenze - čas.

Můžeme tvrdit, že žijeme ve čtyřrozměrném (tzn. 4D) světě, který tvoří tři prostorové dimenze a jedna časová. Někteří fyzici (a není jich úplně málo) však raději hovoří o (3+1)D než o 4D. Abychom se mezi (3+1)D a 4D lépe orientovali, nebude v dalším textu uvažován časový parametr, nýbrž pouze ty prostorové.

Ukazuje se, že pro některé fyzikální a matematické modely jistých jevů více vyhovuje teoretická koncepce většího počtu prostorových dimenzí, než na které jsme zvyklí. Řešení pro diferenciální rovnice popisující tyto jevy nemusí nutně existovat ve 3D, ale může se nacházet ve 4D, 5D atd. Protože neexistuje nic reálného, co by šlo ve 4D (a větším počtu prostorových dimenzí) zobrazit v našem světě, náš mozek má s takovou koncepcí většinou problémy ji korektně vizualizovat a pochopit.

Zkoumat 4D prostor můžeme z několika úhlů pohledu, přičemž je vždy výhodné vycházet z analogií, které již známe pro 2D či 3D. Na displeji přístroje, ze kterého právě čtete tyto řádky (nebo na listu papíru v případě, že jste si text vytiskli), není, technicky vzato, možné vykreslit těleso o více rozměrech, než jsou 2. Důvod je ten, že jak displej monitoru, tak i list papíru (nehledě na lidskou sítnici) jsou v ideálním případě rovněž dvourozměrné (což není v praxi splněno, držme se však pro zjednodušení ideálního stavu, kdy tomu tak je). S projekcí 3D tělesa na 2D prostor se však náš mozek umí vyrovnat - nečiní mu např. problém vnímat Rubikovu kostku (na papíře či displeji, tzn. 2D prostoru) či si s ní dokonce ve formě appletu/simulátoru hrát.

Překvapivé podobnosti

Položme si další záludnou otázku: "Jak z nD udělat útvar nacházející se v (n + 1)D?". Neboli jak z 0D něco dostat do 1D, z 1D do 2D, z 2D do 3D, z 3D do 4D atd.?

0D je prostor, v němž není žádný rozměr. Představujeme si ho jako nekonečně malý bod. Při namalování dvou těchto nekonečně malých bodů je můžeme spojit skrze rozměr (první rozměr je konvenčně označován jako x). Tím vznikne úsečka v 1D.

Pokud vhodně nakreslíme dvě úsečky nad sebe, můžeme je spojit skrze druhý rozměr (pod označením y). Vznikne čtverec ve 2D. Stejně si počínáme i nadále: dva čtverce umístíme za sebe a vzájemně je propojíme skrze třetí rozměr (z). Výsledkem je krychle.

Nic nám nebrání využít stejnou myšlenku i pro další rozměry. Nakreslíme-li dvě vzájemně se nedotýkající krychle, můžeme jejich rohy propojit úsečkami skrze čtvrtý rozměr (w). Vznikne 4D analogie krychle, nazývaná také jako nadkrychle, hyperkrychle anebo teserakt. Familiárně jí v dalším textu bude říkáno 4D kostka (případně 4D analogie kostky), nebo zkrátka NxNxNxN kostka (v tomto případě N = 1).

Konvenčně je stanoveno, že osa x sahá zleva doprava, osa y zezdola nahoru, osa z zezadu dopředu a konečně osu w si můžeme představit jako dolno-od (anglicky down from, někdy se používá řecký výraz kata) až horno-ke (anglicky up toward, můžeme se setkat s řeckým pojmem ana). Všechny 4 osy jsou ve 4D prostoru navzájem kolmé.

Obr. 1 - Konstrukce teseraktu

Vlastnostmi 4D kostky se budeme zabývat později - z obr. 1 nejsou tak pěkně vidět. Vraťme se tak ještě na chvíli ke značení. Míry pro první tři rozměry jsou často nazývány délka, výška / hloubka a šířka - což platí např. u kostky. Jak byste ale nazvali míru v případě 4. rozměru? V angličtině na to mají slovíčko "trength". Dále ve 2D máme obvod a obsah, ve 3D povrch a objem, co ale máme ve 4D? V angličtině se povrch vykreslí na "surcell" (spojení slov surface a cell - viz níže) a objem se vykreslí na "bulk".

Poslední zmínka ke značení: krychle je ve 3D tvořena 6 stěnami, z nichž má každá tvar čtverce (tj. 2D objektu). Teserakt je oproti tomu tvořen 8 stěnami (které jsou ve 4D nazývány nadstěny; v angličtině je užíváno pojmenování cell) a každá z nich má tvar krychle / kostky (tj. 3D objektu).

Hyperkrychle zblízka

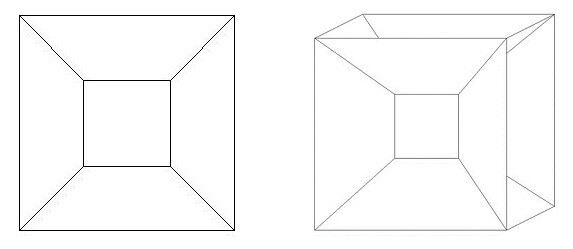
Dozvěděli jsme se, že se 4D analogie krychle skládá z 8 nadstěn. Každá nadstěna je tvořena 3D krychlí o stejném objemu (stejně tak jako každá stěna u 3D krychle je tvořena 2D čtvercem se stejným obsahem). Z toho mj. plyne, že všechny úsečky na teseraktu jsou stejně dlouhé a ve vzájemném úhlu 90° - což je nemožné znázornit ve 3D, proto jsou "vnější" nadstěny na obrázku 2 (a dále) zakřiveny - schválně porovnejte se stěnami krychle v 2D projekci (a měli byste dojít k analogii).

Obr. 2 - zleva: 2D projekce 3D krychle a 4D kostka znázorněna ve 3D (v 2D projekci)

Následující obr. 3 řekne více než tisíc slov a ukazuje 4D kostky 1x1x1x1 (stejně tak jako pravá část obr. 2).

Obr. 3 - Kostky 1x1x1x1

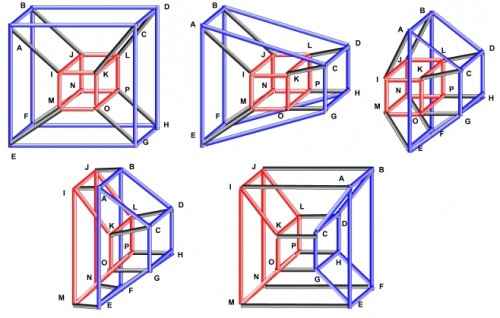
Proč je tedy obr. 1 odlišný od obrázku 3? Je to dáno tím, že na obr. 1 je nakreslen teserakt otočený v prostoru. Staticky to můžeme vyjádřit následným schématem (kde se teserakt otáčí kolem os y a zároveň z).

Obr. 4 - Statická rotace 4D kostky

Dynamicky (animací) lze předchozí obrázek vyjádřit levou polovinou dalšího obrázku (osy, kolem kterých se útvar otáčí, zůstávají stejné, nicméně směr otáčení je opačný). To samé v bledě (no, vlastně světle) modrém, akorát pro osy x a zároveň z, je ukázáno na pravé části.

Obr. 5 - Dynamická rotace 4D kostky

3D kostky mohou rotovat kolem os x, y a z (viz tah x, tah y a tah z ve značení tahů). V případě otáčení kolem osy x rotují stěny R a L na místě, přičemž stěny U, D, F a B rotují ve smyčce. Podobně 4D kostka může rotovat kolem os x a zároveň y, x a zároveň z, x a zároveň w, y a zároveň z, y a zároveň w, nebo z a zároveň w (potom se dvojicím os říká rovina). Z pohledu 3D (viz třeba obr. 3) bude nejmenší nadstěna značena písmenem A, největší pak K, a zbytek písmen lze převzít ze značení ke kostce 3x3x3. Potom, v návaznosti na video níže, pro otáčení kolem os:

• x a zároveň y rotují nadstěny R, L, U a D na místě, přičemž nadstěny F, B, A a K rotují ve smyčce (viz 0:00 - 0:30)
• x a zároveň z rotují nadstěny R, L, F a B na místě, přičemž nadstěny U, D, A a K rotují ve smyčce (viz 0:30 - 1:00)
• x a zároveň w rotují nadstěny R, L, A a K na místě, přičemž nadstěny U, D, F a B rotují ve smyčce (viz 1:00 - 1:30)
• y a zároveň z rotují nadstěny U, D, F a B na místě, přičemž nadstěny R, L, A a K rotují ve smyčce (viz 1:30 - 2:00)
• y a zároveň w rotují nadstěny U, D, A a K na místě, přičemž nadstěny R, L, F a B rotují ve smyčce (viz 2:00 - 2:30)
• z a zároveň w rotují nadstěny F, B, A a K na místě, přičemž nadstěny R, L, U a D rotují ve smyčce (viz 2:30 - 3:00)

Jinými slovy řečeno: uvažujte obyčejného mravence jakožto 2D bytost (čili jeho třetí rozměr zanedbejte). Pakliže ho umístíte na krychli, má na výběr celkem ze tří možností, jak se po ní vydat, jít pořád rovně a dojít do počátečního místa. Tyto tři vzájemně propletené prstence jsou na Rubikově kostce označovány písmeny M, S a E. Řečí písmen značící jednotlivé stěny jde o R L F B, U D F B a R L U D. Pokud budete (jakožto 3D bytost) někdy 4D mimozemšťanem umístěni na teserakt, mohlo by se hodit vědět, že tam se nachází 6 vzájemně propletených prstenců, každý skládající se ze 4 nadstěn - již zmíněné F B A K, U D A K, U D F B, R L A K, R L F B, R L U D.

Nenechte se ale oklamat vlastním mozkem - při otáčení 4D kostky se může zdát, že vnitřní nadstěna je co do objemu menší než ta vnější. Jak již bylo řečeno, všechny jsou totožné (aneb při rotaci 3D krychle se taky nemění obsah jednotlivých stěn). Stejně tak se ani při házení mince nemění její objem, ačkoli tvar se z pohledu pozorovatele mění podle schématu O→()→|→()→O. Totéž je možné pozorovat se stěnami na krychli, která se otáčí kolem jedné osy. Nejinak tomu je i v případě nadstěn u hyperkrychle. Tam se však v průběhu rotace vnitřní nadstěna nachází na pozici vnější nadstěny naruby.

Co z toho vyplývá? Že kdybychom žili ve 4D světě, v jednom úhlu pohledu bychom viděli ostatní tak, jak jsme zvyklí. Pokud by se ale pozorovaní lidé otočili, viděli bychom jejich vnitřní orgány, přičemž ty by se i nadále vzájemně dotýkaly. Lékaři by možná za takový pohled byli rádi, pro zbytek populace by to asi vypadalo poněkud nechutně.

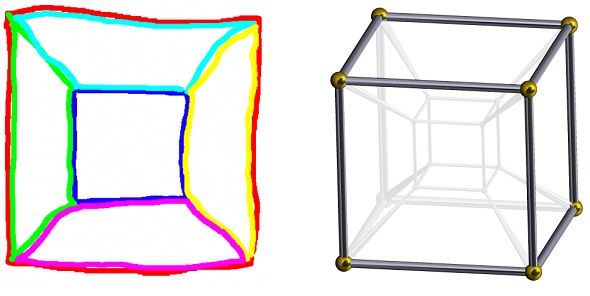
Pro mě osobně je ještě více zajímavější implikace plynoucí z obr. 2. Pokud si ho totiž překreslíme tak, jak je možné vidět na obr. 6, zjistíme, že mozek se nás opět snaží ošálit!

Obr. 6 - Projekce 3D a 4D kostek (do 2D)

Vlevo je znázorněna 3D kostka projektovaná do 2D. Barevně jsou odlišeny jednotlivé stěny (jenž jsou v daném případě průhledné). Na obrázek můžeme pohlížet tak, že červená stěna je nejblíže k očím pozorovatele, zatímco tmavě modrá nejdále. Vpravo máme 4D kostku vyobrazenou ve 3D (a projektovanou do 2D). Nejbližší nadstěna směrem k pozorovateli je vyznačena, zbylých 7 nadstěn je barevně tlumeno (tzn. že jsou znázorněny šedě).

U krychle vlevo se nachází 5 stěn za červenou barvou, a tak se tyto stěny vykreslí dovnitř červeného čtverce. Jsou vzadu ve 3D prostoru, proto jsou vevnitř pro 2D projekci. U teseraktu vpravo je 7 barevně tlumených nadstěn za vnější nadstěnou, tudíž jsou tyto nadstěny namalovány uvnitř (podobně jako u kostky vlevo). Analogicky se těchto 7 nadstěn nachází vzadu (tentokrát však ve čtvrté dimenzi) a to je důvod, proč jsou plně uvnitř pro 3D znázornění. Ačkoli se nám mozek snaží vnutit, že je 7 nadstěn vnitřních, ve skutečnosti (tj. ve 4D) jsou vnější!

Dalším způsobem, jak si můžeme kostku a 4D analogii kostky představit, je použít sítě. Notoricky známá podoba skákacího panáka a vztahy mezi stěnami krychle jsou ve 2D ukázány na levé části obrázku 7. V prostřední části jsou poté ve 3D znázorněny vztahy mezi nadstěnami v případě teseraktu. V obou případech značí barevné čáry dotýkající se části daných objektů. Schéma úplně vpravo můžeme pro zajímavost porovnat s obrázkem 1.

Obr. 7 - Sítě 3D a 4D kostky

Možná vás napadlo: "tož když je možné 3D kostku rozložit do 2D sítě, možná by zrovna tak šly i nadstěny ve 3D rozložit do 2D sítě". A máte pravdu, skutečně to lze udělat. Co se jeví jako intuitivní provedení tohoto úkolu, je nakresleno na levé části následujícího obrázku.

Obr. 8 - Chybná a správná interpretace 2D sítě 4D kostky

Nenaštěstí se nejedná o korektní zobrazení 2D sítě teseraktu, neboť ten je složen z pouze 24 čtverců. Můžete si všimnout, že dvě stěny 3D krychlí v prostřední části obr. 7 jsou vždy společné pro dvě nadstěny, takže z 6·8 = 48 čtverců se stává (6·8)/2 = 24 čtverců - viz pravá část obrázku 8.

Než se pustíme do další kapitoly, možná se mnou budete souhlasit s následujícím výrokem: ve chvíli, kdy si myslíte, že jste 4D prostor pochopili, si uvědomíte, že je ještě o malinko komplexnější, než jste si dosud mysleli. Nabízí se i parafrázovat Sókrata s jeho "vím, že nic nevím". Osobně se mi zdá, že čím více o 4D prostoru vím, tím více o něm vlastně nevím.

4D Rubikova kostka

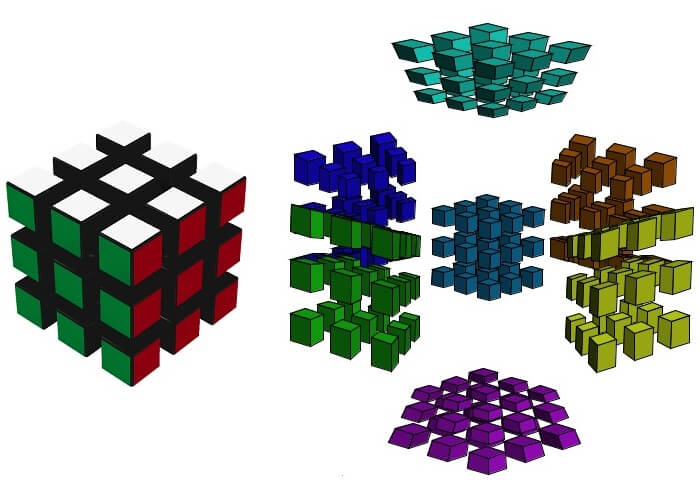
Až doposud byla zmíněna jen 4D analogie krychle. Z hlediska kombinatorických hlavolamů je však zajímavější Rubikova kostka 3x3x3x3. V levé části obr. 9 vidíme složenou klasickou Rubikovu kostku 3x3x3. Vpravo pak 4D Rubikovu kostku, taktéž ve složeném stavu.

Obr. 9 - Složené Rubikovy kostky 3x3x3 a 3x3x3x3

První otázka je nasnadě: "kde je sakra osmá nadstěna u 4D kostky"? Odpověď je (ne)logická, jak už to u čtyř dimenzí bývá: je spojena se všemi šesti okolními nadstěnami (kromě té s vodovou barvou nacházející se uprostřed), ale na opačných stěnách než v případě vodové nadstěny - nachází se zároveň vlevo, vpravo, vepředu, vzadu, nahoře i dole. Protože je obtížné znázornit tuto představu ve 3D v daném pohledu (a navíc by to bylo extrémně matoucí pro náš mozek ve zvolené projekci - viz obrázek 20 dále), osmá nadstěna 3x3x3 je zkrátka neviditelná. Může se ale dostat na nynější pozici vodové nadstěny vhodnou dvojnásobnou rotací hlavolamu jako celku, nebo na pozici jakékoli další nadstěny vhodnou jednoduchou rotací hlavolamu - jak plyne z videa pod obr. 5.

Lze si všimnout, že každá nadstěna má jednu barvu (stejně tak jako každá stěna Rubikovy kostky 3x3x3 má ve složeném stavu rovněž jednu barvu). Zatímco jedna stěna kostky 3x3x3 je tvořena devíti (3·3) 2D nálepkami, jedna nadstěna u 3x3x3x3 je tvořena 27 (3·3·3) 3D nálepkami. Obecně pak "stěny" na D-rozměrné kostce mají nálepky (D-1)-rozměrné.

Zopakujme si, že kostka 3x3x3 se skládá z:

• 6 jednobarevných středů
• 12 dvoubarevných hran
• 8 trojbarevných rohů

4D kostka 3x3x3x3 obsahuje následující dílky:

• 8 jednobarevných středů
• 24 dvoubarevných hyper-středů
• 32 trojbarevných hyper-hran
• 16 čtyřbarevných hyper-rohů

Obr. 10 - Vlevo: zvýrazněný střed; vpravo: zvýrazněný hyper-střed

V obou případech (3x3x3 i 3x3x3x3) platí, že dílky označeny jako "středy" jsou vzájemně vůči sobě neměnné. Určují tudíž barvu stěny, resp. nadstěny.

Obr. 11 - Vlevo: zvýrazněná hyper-hrana; vpravo: zvýrazněný hyper-roh

Proč zrovna čísla 8, 24, 32 a 16 z hlediska počtu dílků? Inu, protože vyšla při dosazení do obecného vzorce :-). Nejprve však trocha teorie: všeobecně platí, že D-rozměrná Rubikova kostka ve tvaru 3^D má D+1 typů dílků, obsahující 0, 1, 2 ... D rozdílných barevných nálepek. Pro 3x3x3 se jedná o 1 dílek, který má 0 nálepek (v reálné kostce jde o osový kříž), 6 dílků mající 1 nálepku, 12 dílků mající 2 nálepky a konečně 8 dílků mající 3 nálepky. Slibovaný vzoreček na počet typových dílků v závislosti na počtu různobarevných nálepek pro Rubikovu kostku tvaru 3^D má podobu:

kde N značí počet nálepek na daném typu dílku, D znázorňuje počet dimenzí hlavolamu a vykřičník představuje faktoriál. Pro zajímavost je přiložena i přehledná tabulka pro hodnoty D i N v rozmezí 0 až 10.

Zobecněním vzorce napsaného výše může být formule pro počet typových dílků v závislosti na počtu dělících řezů v jednom směru na stěnu + 1 (tj. 3 dělící řezy v jednom směru + 1 = 4 pro Rubikovu kostku 4x4x4, 4 dělící řezy v jednom směru + 1 = 5 pro kostku 5x5x5 atd.) pro Rubikovu kostku ve tvaru A^D (kde A udává počet dělících řezů v jednom směru na stěnu + 1). Poté můžeme psát:

Obr. 12 - Rubikovy kostky 3x3, 3x3x3, 3x3x3x3 a 3x3x3x3x3

Dá se početně ukázat, že Rubikova kostka 3x3x3x3 může mít téměř 1,8·10¹²⁰ různých pozicí (oproti "jen" 4,3·10¹⁹ v případě kostky 3x3x3). Pro teserakt 4x4x4x4 už existuje více než 1,3·10³³⁴ odlišných pozicí (ve srovnání s "jen" 7,4·10⁴⁵ a kostkou 4x4x4). Kostka 5x5x5x5 pak může zaujímat jednu ze svých více než 8,2·10⁷⁰⁰ různých pozic (v porovnání s 2,8·10⁷⁴ pozicemi pro kostku 5x5x5). Číslo 8,2·10⁷⁰⁰ už je nepředstavitelné (zajisté se s tak velkými čísly nesetkáváme každý den), ale pořád není nic ve srovnání s počtem pozic Rubikovy kostky 150x150x150. V kontrastu s tím 2D Rubikova kostka 3x3 uvedená na obrázku výše má pouze 4 možné orientace a nemůže být dokonce ani rozmíchána.

Věřím, že skládání 3x3x3x3 je principiálně stejné jako 3x3x3 (alespoň z hlediska komutátorů a konjugací) - o tom mimo jiné svědčí i to, že někteří fajnšmekři dokonce skládají 4D hlavolamy poslepu (v takovém případě se po prvním tahu na simulátoru hlavolamu změní všechny nálepky na šedé). Nicméně díky tomu, že se ve 4D analogii vyskytují i jiné typy dílků (s předponou "hyper"), může při řešení docházet k zajímavým situacím. Jedna z nich je znázorněna na obrázku níže. Jedná se o špatnou orientaci (resp. 4D otočení) pouze jednoho hyper-rohu, která vznikla spojením dvou 3D rotací. První byla provedena kolem tmavě-modré "osy" (tzn. osy x), načež byla provedena i kolem vodově barevné "osy" (tzn. osy y), což vyústilo k výměně zelené s tmavě-modrou nálepkou a světle-modré s nálepkou vodové barvy.

Na druhou stranu na tom není nic, co bychom neznali z kostky 3x3x3. U ní jsou dostupné jen 2D rotace kolem 3D os. Pokud např. chceme orientovat / natočit roh UFR, můžeme provést tah F, následovaný tahem R. Tyto dvě 2D rotace mají z hlediska rohů za následek 3D otočení rohu na pozici UFR. Jediným rozdílem mezi kostkou 3x3x3 a 3x3x3x3 je to, že u druhé jmenované jsou dostupné pouze 3D rotace kolem 4D os. Myšlenka však zůstává neměnná - provedení dvou 3D tahů, které formují 4D orientaci / natočení hyper-rohu.

Obr. 13 - Složený hlavolam až na 1 hyper-roh

Monstróznější monstrozity

Komu skládání 4D analogie Rubikovy kostky 3x3x3 přijde pod jeho úroveň, může přidat další rozměr (technikou, kterou je možné vidět na obr. 1 - propojením dvou teseraktů), čímž vznikne 5D analogie Rubikovy kostky 3x3x3, která bude mít celkem 810 nálepek. Lze však v trendu pokračovat dál a vytvořit 6D nebo 7D Rubikovu kostku (jejichž konstrukce, stejně tak jako vazby mezi jednotlivými dílky, si už osobně nedokážu představit).

Na obr. 14 je údajně znázorněna složená Rubikova kostka 3x3x3x3x3x3x3. Tedy alespoň 7 z jejích 14 stěn (kde jednou stěnou je míněna Rubikova kostka 3x3x3x3x3x3).

Obr. 14 - 7D Rubikova kostka 3x3x3 ve složeném stavu

Z nudné složené pozice ji můžeme zamíchat. Pak bychom viděli něco podobného, jako je ukázáno na obr. 15.

Obr. 15 - 7D Rubikova kostka 3x3x3 v rozmíchaném stavu

Pokud si myslíte, že najít skládaný dílek v této změti barev je skoro nadlidský úkol, nezbývá mi, než s vámi souhlasit. Navíc jedna věc je ho najít a druhá pak opravdu složit. Jen hrstka lidí na Zemi to dokázala pro všech 2 172 pohyblivých dílků na hlavolamu se vyskytujících, což znamená, že správně umístili i orientovali všech 10 206 viditelných nálepek (obě uvedené hodnoty lze vyčíst z tabulky výše).

Hlavolam 7D analogie Rubikovy kostky 3x3x3 má více než 3,3·10⁸⁹³⁵ různých pozic, z nichž je samozřejmě tahle hračka složená jen při jedné z nich.

Mezi mňamkózní věcičky dozajista patří i 7D analogie Rubikovy kostky 5x5x5. Ta obsahuje 78 110 pohyblivých dílků a 218 750 viditelných nálepek. Počet pozic tohohle mazlíka je číslo o téměř 227 000 číslicích (asi). Rubikova kostka 3x3x3 se svými 20 číslicemi tady působí více než směšně.

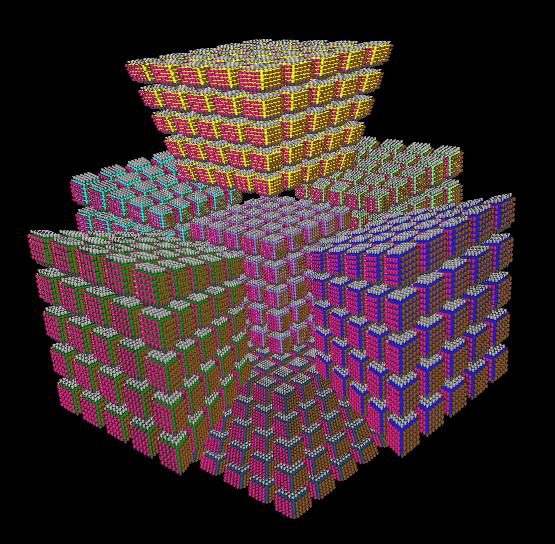
Obr. 16 - 7D Rubikova kostka 5x5x5 ve složeném stavu

A jedna třešnička na závěr. 4D analogii Rubikovy kostky jsme už viděli. Co takhle ukázat i 4D analogii hlavolamu Megaminx? Ta se skládá ze 120 nadstěn a každá z nich má tvar hlavolamu Megaminx (tzn. dvanáctistěnu). Najdeme zde 2 641 dílků, 7 560 nálepek a 2,3·10⁸¹²⁶ odlišných pozic. Jak velké tohle číslo je? Zaprvé hodně. Zadruhé si zkuste představit, že každá částice ve vesmíru je malinký vesmír se stejným počtem částic, jako je v našem vesmíru. To je o mnoho víc částic, což? Nyní si představte, že všechny částice ve všech těch vesmírech jsou jen dalším vesmírem pro stejný počet částic, jako je v našem vesmíru. To už dělá pořádně velké číslo všech částic, není-liž pravda? No a teď celý proces opakujte ještě více než 100x a přiblížíte se k počtu pozic, které mohou nastat na 4D analogii hlavolamu Megaminx.

Obr. 17 - Složená 4D analogie hlavolamu Megaminx

Níže je hlavolam rozmíchaný. Zároveň byly z pohledu pro lepší názornost odříznuty některé jeho části.

Obr. 18 - Rozmíchaná 4D analogie hlavolamu Megaminx

Prostor pro lámání si hlavy

Podnětem ke zpracování celého tohoto článku byla jednoduchá úvaha. Napadlo mě, že když udělám částečně transparentní (tj. průhlednou) jednu stěnu Rubikovy kostky, budu schopen při určitém natočení hlavolamu vidět na jeden pohled všech 6 stěn, které se na kostce vyskytují. V tu dobu jsem se zrovna koukal na simulátor 4D analogie kostky a tak byl jen krůček k myšlence, jak vidět celou 3x3x3x3 také jen na jeden pohled bez nutnosti s hlavolamem otáčet skrze 4. dimenzi.

To se postupem časo ukázalo jako ne úplně snadný úkol a tak jsem usoudil, že bude lehčí, když zprvu zhlédnu rotaci 3x3x3x3 kolem nějakých jejích os, stejně jako to je v případě 1x1x1x1 možné pozorovat na obrázku 5. I když nevidím důvod, proč by takový koncept nemělo jít nakreslit / animovat, nejsem schopný toho dosáhnout. Druhá myšlenka (tj. rotace 3x3x3x3 kolem dvou svých os) tudíž stále čeká na svou realizaci, příp. vyvrácení.

Vraťme se tak k počátečnímu nápadu vidění celého 4D hlavolamu bez nutnosti jeho rotace ve čtvrtém rozměru. Za tímto účelem může sloužit např. obrázek 19, kde se nachází 4D analogie Rubikovy kostky 2x2x2. Pokud budeme uvažovat osu souřadnic (w, x, y, z), potom červená nadstěna (viz levá část obrázku) má souřadnice (1, 0, 0, 0), a zároveň olivová nadstěna (viz pravá část obrázku) má souřadnice (-1, 0, 0, 0).

Obr. 19 - Rubikova kostka 2x2x2x2

Tyto dva pohledy umožňují vidět všech 8 nadstěn a zároveň je zřejmé, jaké jsou mezi nimi vztahy. Jenže já chtěl původně jen jeden pohled. V souladu s prvním odstavcem pod obr. 9 tak můžeme vykreslit osmou nadstěnu pro teserakt 3x3x3x3 následujícím způsobem:

Obr. 20 - Transparentní nadstěna u Rubikovy kostky 3x3x3x3

Jak již bylo zmíněno, náš mozek není předurčen k tomu, aby jednoduše rozeznal vztahy nadstěn v teseraktu, když bude jedna nadstěna částečně transparentní. Proto jsem ani s tímto pohledem nebyl spokojen. Kamarád Brandon mi posléze ukázal další možnost projekce, ve které je vidět všech 8 nadstěn, přičemž ani jedna z nich není průhledná.

Obr. 21 - Všechny nadstěny Rubikovy kostky 3x3x3x3 v jednom pohledu

Přestože vím, co vidím, přiznávám na rovinu, že tohle nejsem schopen interpretovat. Jako by vše, co bylo až do této chvíle řečeno, náhle přestalo platit. Může za to natočení ve 4D, které prostě náš mozek (alespoň ten můj) nebere. Kéž by pro tento pohled mohl být zachován "klasický tvar" a ne tahle obluda připomínající pyramidu... Když už nic jiného, je ale pěkně vidět, že žádná nadstěna neleží uvnitř nějaké jiné nadstěny (v kontrastu např. s obrázkem 20).

Jako nejlepší si mi proto jeví zozbrazit všech 8 nadstěn do jednoho pohledu pomocí sítě, složené z 3D kostek 3x3x3.

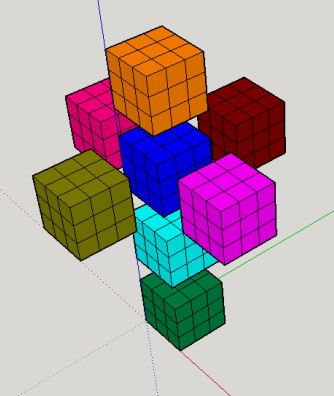
Obr. 22 - 8 nadstěn v podobě 3D sítě

Největší výhodu této projekce shledávám v tom, že lze hlavolamem otáčet ve 3D prostoru - což je činnost, kterou náš mozek dokáže vnímat bez sebemenších problémů. Navíc jsou vždy vidět všechny nadstěny pouze v jednom pohledu. Dochází tak k naplnění cíle, kterého jsem chtěl původně dosáhnout.

Protože při tahu (např. U) na Rubikově kostce 3x3x3 se pohybuje 9 (3·3) dílků, jeden tah na 4D Rubikově kostce má za následek pohyb 27 (3·3·3) dílků. Ty jsou v návaznosti na obr. 22 zobrazeny na obr. 24 (tam byl proveden 4D analogický tah k tahu U, známého ze 3D kostky). Pakliže u kostky 3x3x3 pohnete jednou stěnou, z hlediska barevných nálepek se budou pohybovat i některé z těch, které s danou stěnou sousedí - to je vidět z obr. 23, kde zelená stěna byla při pohledu shora nejblíže k nám a byl udělán tah U'.

Obr. 23 - Síť Rubikovy kostky 3x3x3 po 1 tahu

Pokud u kostky 3x3x3x3 pohnete jednou nadstěnou, z hlediska barevných nálepek se budou pohybovat i některé z těch, které s danou nadstěnou sousedí. Připomeňme si, že u obou hlavolamů zůstavá střed v průběhu tahu na svém místě.

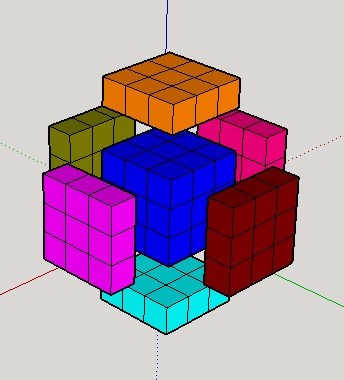
Obr. 24 - 27 dílků, které se při 1 tahu na kostce 3x3x3x3 pohybují

Vlastní ideou, u níž si však nejsem jistý její realizací, je zavedení pohledu, kde nebude vidět všech 8 nadstěn, nýbrž pouze 7 z nich a ta osmá bude zobrazena bez nutnosti dělat rotaci hlavolamu ve čtvrté dimenzi. Protože 7 nadstěn není problém do projekce namalovat, zbývá vyřešit otázku, jak ztvárnit osmou barvu nadstěny do tohoto konceptu. Na jednu nálepku v případě kostky 3x3x3 jsme schopni umístit vícero barev. Pakliže tak učiníme, vznikne Supercube.

Obr. 25 - Supercube 3x3x3

Zeptejte se mě, jak by vypadala 3x3x3x3 ve formě Supercube - nevím. Ve složeném stavu by ale, s přihlédnutím k obr. 22, nemusela být vůbec namalována zelená nadstěna (která je stejnak např. na třetí pozici zleva na obr. 12 skrytá / neviditelná). Bylo by však zapotřebí tuto zelenou barvu umístit na některé další dílky (vyjma ty s modrými nálepkami) na hlavolamu. Tahy by potom navíc vypadaly poměrně neuspořádaně, protože by se při každém z nich měnily barvy na jednotlivých dílcích obsažených - tzn. že jeden a ten samý dílek by měl po tahu č. 1 určité barvy, ale po tahu č. 2 (úhel pohledu na hlavolam by zůstal neměnný) by měl barvy jiné. Je to asi jako s rotujícím teseraktem NxNxNxN (kde N > 1) - ačkoli teoreticky nevidím důvod, proč by to nemělo fungovat, fakticky si to představit nedokážu.

Když jsou dva rozměry příliš

Poslední kapitola bude důkazem toho, že 3D útvary jdou netradičně znázornit i ve 2D. Na obrázku 23 byla uvedena hojně používaná 2D síť Rubikovy kostky 3x3x3. Napadlo by vás někdy, že se dá vyjádřit i tak, jak je ukázáno na levé části obr. 26 (tam má hlavolam místo krychle tvar koule)? Vpravo je nápověda, jak takové vyobrazení vlastně vzniklo.

Obr. 26 - Netradiční vyobrazení Rubikovy kostky 3x3x3

Ve stejném duchu můžeme zobrazit i Megaminx nebo Rubikovu kostku 5x5x5.

Obr. 27 - Sítě pro Megaminx a Rubikovu kostku 5x5x5

Na obrázku níže je znázorněna i síť pro hlavolam Petaminx, což je čtyřvrstvý Megaminx. Následuje ilustrativní video, které slouží k získání rámcové představy, jaké dílky se kam pohybují při udělání jednoho tahu.

Obr. 28 - Netradiční síť hlavolamu Petaminx

Není tomu tak dávno, kdy jsem se před kamarádem Tomem (který jinak s kombinatorickými hlavolamy nemá nic společného) zmínil o tom, že se snažím pochopit 4D kostku. Jeho reakce mě docela uzemnila. Odpověděl něco v tom smyslu, že dokázal na papír nakreslit 16D kostku.

V duchu jsem si pomyslel "jasně, jen kdybys nekecal...". Druhý den mi ukázal skicu, kterou kreslil jednou rukou, zatímco tou druhou odpovídal na jakýsi e-mail. Proto je jeho neumělecká čmáranice naprosto ospravedlnitelná.

Obr. 29 - Kostka ve 3D a 2D

Nahoře vidíme něco, co má znázorňovat kostku. Čtyři rohy jsou vyznačeny puntíky, na další 4 už nezbyl čas je označit :-). Dole je všech 8 puntíků představující všech 8 rohů. Ty bývají spojeny hranami (nahoře ve tvaru úsečky, dole ve tvaru půlkružnice). Můžeme si všimnout, že každý roh je spojen se třemi dalšími a to je důvod, proč z jednoho puntíku vedou vždy tři půlkružnice. Toť vše. Jednoduché a elegantní.

Nakreslením dvou takových směsicí půntíků s půlkružnicemi a vytvořením dalších půlkružnic, které spojují patřičné (hyper) rohy skrze další rozměr, dojde k vytvoření 4D kostky. Obdobně jako tomu bylo ukázáno na obr. 1. Tomův výklad je sice daleko náročnější na představivost (už jen díky tomu, že půlkružnice nejsou proporcionální co do velikosti, nebo i zásluhou toho, že všechny rohy leží na jedné přímce), ale zato musím uznat, že měl asi pravdu - takovýmto způsobem je opravdu možné vytvořit kostku o mnoha rozměrech. Údajně skončil u 16D, protože pak už něměl na papíře místo (prý použil formát A3).

Existuje mnoho simulátorů Rubikovy kostky 3x3x3, u kterých můžeme jedním pohledem vidět všech jejích 54 nálepek. Jeden takový exemplář lze pozorovat na obr. 30 vlevo. Naproti tomu jsou k dispozici i "realističtější" simulátory, které v jednom pohledu nedovolují vidět veškeré dílky na hlavolamu - viz například obr. 30 vpravo.

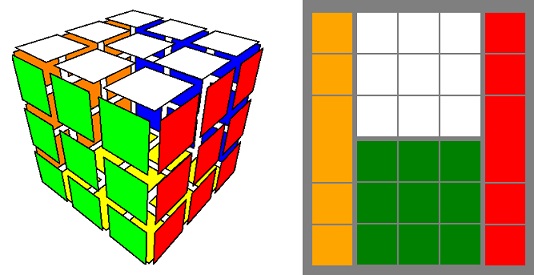
Obr. 30 - Dva různé simulátory Rubikovy kostky

Na pravé části obr. 30 je čelní stěna zelená, horní stěnu tvoří bílé nálepky. Dále jsou patrné i oranžové a červené nálepky, přičemž 2 velké bloky představují dvě barvy nálepek rohů. Celkově tudíž můžeme jedním pohledem pozorovat 5 hran, 2 středy a 2 rohy (a potom i části 2 dalších hran a 4 rohů).

Ačkoli ani jeden případ nelze zcela ztotožnit s pohledem na kostku známým z praxe, nejrychlejší lidé dokáží obě dvě projekce vyřešit během několika málo sekund. To ostatně platí i pro reálný hlavolam.

Graficky stránku obohatili (odkazy platné k 9. 3. 2015):

Obr. 1 - https://en.wikipedia.org/wiki/Hypercube
Obr. 2, 3 (vpravo) - http://cr4.globalspec.com/blogentry/23006/Rubik-s-Hypercube-Newsletter-Challenge-August-2013
Obr. 3 (vlevo) - http://www.shapeways.com/product/Z2JLWWP3X/hypercube-a
Obr. 4 - http://www.kastellorizo.org/puzzles/4Ds
Obr. 5 vlevo - https://cs.wikipedia.org/wiki/%C4%8Ctvrt%C3%BD_rozm%C4%9Br
Obr. 5 vpravo - http://www.mathematik.com/4DCube/4DCubePovray.html
Obr. 6, 8 (vlevo), 13, 19, 20, 21, 22 - http://twistypuzzles.com/~sandy/forum/viewtopic.php?f=8&t=27375
Obr. 7 (vlevo a uprostřed) - http://forums.xkcd.com/viewtopic.php?t=21376
Obr. 7 (vpravo) - https://en.wikipedia.org/wiki/Four-dimensional_space
Obr. 8 (vpravo) - http://www.magic-squares.net/c-t-htm/t_unfolded.htm
Obr. 9 (vlevo) - https://www.randelshofer.ch/cubetwister
Obr. 9 (vpravo), 10, 11 - http://superliminal.com/cube/cube.htm
Obr. 12 - http://www.gravitation3d.com/magiccube5d/anatomy.html
Obr. 14, 15, 16 - http://astr73.narod.ru/MC7D/MC7D.html
Obr. 17, 18 - http://www.gravitation3d.com/magic120cell/index.html
Obr. 24 - osobní korespondence s uživatelem rayray_2561 na fóru http://www.twistypuzzles.com/forum
Obr. 25 - https://sites.google.com/site/twistykon/home/new-in-2011
Obr. 26, 27, 28 - http://www.gravitation3d.com/magictile
Obr. 29 - kamarád Tom
Obr. 30 (vlevo) - https://www.ocf.berkeley.edu/~jfly/projects/qqTimer/qqTimer.htm
Obr. 30 (vpravo) - http://mzrg.com/js/qcube-v2.html